Matemáticas para predecir el comportamiento de cultivos en microbiología

08 May Matemáticas para predecir el comportamiento de cultivos en microbiología

• La tesis de Javier López de la Cruz, “Sistemas dinámicos  en  modelos estocásticos  con  ruido  fraccionario” estudia modelos con futuras aplicaciones a la mejora del cultivo de bacterias o levaduras.
• Empleando esta técnica se puede mantener un cultivo en suspensión en condiciones óptimas durante un largo período de tiempo

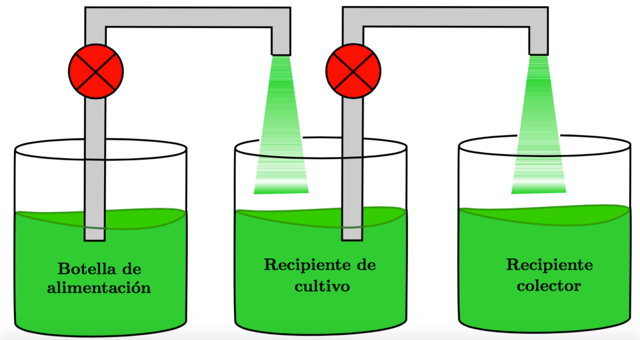
Esquema de un quimiostato

El quimiostato es un tipo de cultivo continuo de microorganismos en suspensión. Mantener un ambiente uniforme y adecuado para los microorganismos es importante para conseguir el rendimiento óptimo del cultivo, para ello se estudia cómo varían las cantidades de nutrientes y de microorganismos con el paso del tiempo. Así por ejemplo, se cultivan las levaduras para las panaderías o las bacterias para producir antibióticos como la penicilina.

Los sistemas de ecuaciones diferenciales (dx/dt=f(t,x)) sirven para predecir estos procesos de la biología y ofrecen datos sobre cómo se comportará el cultivo cuando haya pasado mucho tiempo. En el modelo más sencillo, existen parámetros que permanecen constantes durante todo el proceso, como el flujo (D) con el cual se pasa el nutriente del primer tanque al recipiente de cultivo, que coincide con el flujo con el cual se elimina el excedente al tercer tanque.

Tal exactitud mantenida en el tiempo es difícil de obtener en el laboratorio, donde las situaciones no son ideales y ocurren sucesos inesperados que los científicos no pueden controlar, como que la bomba que controla el flujo se obstruya con pequeñas partículas de suciedad. En este caso, el flujo cambia pero es imposible conocer cuánto ni por cuánto tiempo; la variable flujo ha pasado de ser una variable constante completamente determinada a ser una variable aleatoria, por tanto el modelo que describe el proceso de quimiostato ha pasado de ser un modelo determinista a ser un modelo estocástico. El problema: predecir condiciones sobre los parámetros del modelo bajo las cuales se consigue persistencia de los microorganismos.

¿Qué son los modelos estocásticos matemáticos aplicados a procesos biológicos?

Modelar significa representar procesos reales con sistemas de ecuaciones diferenciales, con el fin de predecir cómo evoluciona con el tiempo. Javier López de la Cruz, especialista en los campos del  Análisis  Matemático  y  la  Matemática Aplicada en el IMUS, ha estudiado durante 4 años de su tesis la dinámica de los procesos de quimiostato cuando sufren perturbaciones. Si tenemos en cuenta las perturbaciones (inconvenientes inesperados) que pueden surgir al desarrollar un experimento, es posible obtener modelos matemáticos mucho más realistas desde el punto de vista biológico.

Volviendo al ejemplo de un flujo aleatorio, Javier ha estudiado el comportamiento con dos modelados distintos, uno hace uso del proceso de Wiener y otro del proceso de Ornstein-Uhlenbeck. El proceso de Wiener describe los movimientos de una partícula cuando se encuentra totalmente sumergida, y es el modelado que suele aplicarse. Sin embargo, no es del todo realista porque cuando pasa el tiempo, aparecen variables que toman valores negativos, lo cual no tiene sentido desde el punto de vista biológico.

Sin embargo empleando el proceso de Ornstein-Uhlenbeck, es posible obtener perturbaciones controladas, como ocurre en la realidad, de tal forma que las concentraciones de nutrientes y microorganismos estén alejadas del cero y dentro de ciertos conjuntos, independientemente de cómo sea la perturbación (lo que en matemáticas se describe como la existencia de conjuntos absorbentes y atrayentes de las soluciones del sistema diferencial que describe el modelo). Esto permite obtener condiciones que aseguren que el tanque estará en condiciones óptimas para albergar las bacterias durante mucho tiempo, algo que nunca antes se había demostrado.

Para llevar a cabo la comparación de los modelos resultantes, las técnicas matemáticas utilizadas están principalmente basadas en la teoría clásica de Ecuaciones Diferenciales Ordinarias, así como en la moderna teoría de los Sistemas Dinámicos Aleatorios y los atractores pullback.

La matemática aplicada promueve la multidisciplinariedad de las ciencias

 En los últimos años la investigación científica está cobrando mayor relevancia y, en concreto, el campo de la Matemática Aplicada está ganando a una vertiginosa velocidad un enorme interés entre la comunidad de investigadores ya que nos permite poder ser capaces de modelar de manera fiel y, con ello, explicar un gran número de situaciones de la vida real con origen en una multitudinaria diversidad de ámbitos: física, medicina, biología y química, por citar algunos.